Let's try to solve this sudoku in APL:
| 6 | ||||||||
| 4 | 8 | 7 | 5 | |||||
| 9 | 1 | 3 | 8 | |||||
| 8 | 9 | |||||||
| 7 | 6 | 5 | 8 | 4 | ||||
| 2 | 8 | |||||||
| 2 | 3 | 1 | 4 | |||||
| 1 | 5 | 9 | 8 | |||||
| 7 |
Note: You can read more about sudokus elsewhere on this homepage.
We represent the problem as a 9x9 matrix. In order to make it easier to get problems in and out of the APL system we start by defining two help functions:
G z[a2n a
;1' z[ 9 9 R@1-K0123456789KIa
G
G z[n2a n
;1' z[K0123456789K;1-,n'
G
We can create the matrix O1 like this:
o1[a2n K000060000400807005009103800080000090700658004020000080002301400100509008000070000K
o1
0 0 0 0 6 0 0 0 0
4 0 0 8 0 7 0 0 5
0 0 9 1 0 3 8 0 0
0 8 0 0 0 0 0 9 0
7 0 0 6 5 8 0 0 4
0 2 0 0 0 0 0 8 0
0 0 2 3 0 1 4 0 0
1 0 0 5 0 9 0 0 8
0 0 0 0 7 0 0 0 0
The unknown positions are represented by zeros.
We will now try to find the digits 1-9 that must replace the zeros so that the digits 1-9 occur once in each row, column, and 3x3 submatrix.
We use this simple algorithm:
Let's see how this can be done:
We call the matrix with the puzzle m, and we find the row number r of the first zero:
r[:D/m"I0
The expression D/m gives us the minimum value in each row, and the following I0 looks for a zero in this list. It will return 10 if no zero is found. This gives us the first line in the program:
;1' {::r[:D/m"I0"$9"/l1
which means: Assign the row number of the first occuring zero to r and jump to the label l1 if r is less than or equal to 9.
The compression operator / is often used together with conditional branches:
0/17
1/17
17
So the statement {:r$9"/17 means go to line 17 if r$9 else continue with the next line in the program. It is convenient to use symbolic labels for branches in APL as line numbers are renumbered automatically when lines are removed or inserted. Labels are local variables that automatically are given the value of the line number in which they occur when the program starts.
The next lines print m as the solution, a blank line, and exits the program:
;2' m
;3' I0
;4' {0
We now must find the column number, c, of the first zero occurring in row r:
;5' l1>c[m;r<'I0
This line contains the label l1 we referred to in line no. 1.
Now the fun part begins: We join all the numbers from row r with column c together with the numbers from the 3x3 submatrix that contains the element m;r<c':
m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'
Let's try this for row 1, column 1 (the first zero in the example):
m[o1
r[1
c[1
m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'
0 0 0 0 6 0 0 0 0 0 4 0 0 7 0 0 1 0 0 0 0 4 0 0 0 0 9
We use the membership operator E to see which of the numbers 1-9 that exist in this list:
:I9"E:m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'"
1 0 0 1 0 1 1 0 1
We can see that the list contains the numbers 1, 4, 6, 7, and 9. But we are interested in the numbers that does not exist, so we negate the answer:
T:I9"E:m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'"
0 1 1 0 1 0 0 1 0
We are now ready to use the compress operator to get the list of possible candidates:
:T:I9"E:m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'""/I9
2 3 5 8
So we have to try the numbers 2, 3, 5, and 8 as candidates in the first cell.
So we have the next line ready for the program:
;6' i[Rt1[:T:I9"E:m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'""/I9
We assign the result list to the variable t1 and the length of t1 to i.
If i is zero we have come to a dead end and we exit the program. This gives us the next line of the program:
;7' l2>{:i%0"/0
This line has the label l2, we'll need this in a little while.
We must now prepare a copy of the matrix m and insert the numbers from the list t1 into row r, column c. We do it like this:
;8' m1[m
;9' m1;r<c'[t1;i'
;10' sudoku m1
;11' i[i_1
;12' {l2
We start from the end of the list t1 by inserting t1;i' into m1;r<c', call the program again, and count down i.
That's it! The whole program looks like this:
G sudoku m<r<c<m1<t1<i
;1' {::r[:D/m"I0"$9"/l1
;2' m
;3' I0
;4' {0
;5' l1>c[m;r<'I0
;6' i[Rt1[:T:I9"E:m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'""/I9
;7' l2>{:i%0"/0
;8' m1[m
;9' m1;r<c'[t1;i'
;10' sudoku m1
;11' i[i_1
;12' {l2
G
Note that the declaration line contains <r<c<m1<t1<i after the parameter m, this is a list of the variables that are local to this program.
Does it work?
sudoku o1
8 1 7 2 6 5 9 4 3
4 6 3 8 9 7 2 1 5
2 5 9 1 4 3 8 7 6
6 8 4 7 3 2 5 9 1
7 9 1 6 5 8 3 2 4
3 2 5 9 1 4 6 8 7
5 7 2 3 8 1 4 6 9
1 4 6 5 2 9 7 3 8
9 3 8 4 7 6 1 5 2
Yes, it does! We can copy the function time from the workspace advancedex in public library 1 to measure the CPU time it takes to run:
"copy 1 advancedex time
saved 16.41.30 09/06/72
and reset the timing variable timer. Calling time will display the number of minutes, seconds, and 1/60's seconds since last call:
timer[0
time
0 38 53
time
0 0 0
Lets time the sudoku program:
time
0 0 0
sudoku o1
8 1 7 2 6 5 9 4 3
4 6 3 8 9 7 2 1 5
2 5 9 1 4 3 8 7 6
6 8 4 7 3 2 5 9 1
7 9 1 6 5 8 3 2 4
3 2 5 9 1 4 6 8 7
5 7 2 3 8 1 4 6 9
1 4 6 5 2 9 7 3 8
9 3 8 4 7 6 1 5 2
time
0 39 25
It takes nearly 39.5 seconds on my laptop.
This algorithm does not work very well if there are many zeros in the puzzle. It can take hours to finish.
We shall make improvements to this in the next chapter.
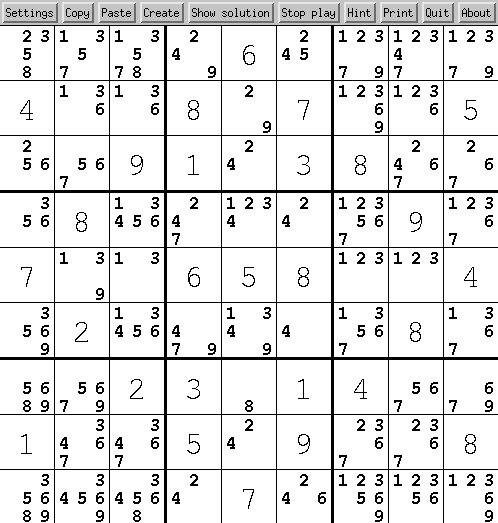
When I solve sudoku's with my own program it looks like this:

The small numbers in the empty cells are the possible candidates for this cell. You can recognize the numbers 2, 3, 5, and 8 we found for the first cell.
But you see also something else: Two of the cells have only one candidate, cells o1;6<6' and o1;7<5'. It would be a good idea to start with these cells instead of just taking the first zero in the puzzle.
Also note that in row 5, number 9 occurs only once.
In column 5, number 8 occur once. In column 6, the numbers 5 and 6 occur only once.
In the second submatrix, o1;I3<3-I3', the number 5 occurs only once. And in the eights submatrix, o1;6-I3<3-I3', the numbers 6 and 8 occur only once.
How can we get this information in APL?
We now call the matrix to be investigated m.
We start by making a help table with 81 rows and 27 columns.
One row for each cell in the puzzle.
The first 9 columns in the table row ::r_1"=9"-c contains the 9 numbers from row r.
The next 9 numbers in this row contains the 9 numbers from column c.
The last 9 numbers contains the numbers from the submatrix m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'.
t1[m;,Þ 9 9 RI9<'
t1[t1,Þm;<81RI9'
t1[t1,:9 9 R 1 3 2 4 Þ 3 3 3 3 Rm";, 2 4 1 3 Þ 3 3 3 3 RI9<'
Let's see how the indices are calculated:
,Þ 9 9 RI9
1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 4 4 4 4 4 4 4 4 4
5 5 5 5 5 5 5 5 5 6 6 6 6 6 6 6 6 6 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8
8 8 9 9 9 9 9 9 9 9 9
81RI9
1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7
8 9 1 2 3 4 5 6 7 8 9
, 2 4 1 3 Þ 3 3 3 3 RI9
1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6
4 4 4 5 5 5 6 6 6 4 4 4 5 5 5 6 6 6 7 7 7 8 8 8 9 9 9 7 7 7 8 8 8 9
9 9 7 7 7 8 8 8 9 9 9
The first list is the row numbers for the rows to be inserted, the second list is the column numbers, and the last list is the submatrix numbers.
We use this smart transformation to convert from submatrix to row format:
m
0 0 0 0 6 0 0 0 0
4 0 0 8 0 7 0 0 5
0 0 9 1 0 3 8 0 0
0 8 0 0 0 0 0 9 0
7 0 0 6 5 8 0 0 4
0 2 0 0 0 0 0 8 0
0 0 2 3 0 1 4 0 0
1 0 0 5 0 9 0 0 8
0 0 0 0 7 0 0 0 0
9 9 R 1 3 2 4 Þ 3 3 3 3 Rm
0 0 0 4 0 0 0 0 9
0 6 0 8 0 7 1 0 3
0 0 0 0 0 5 8 0 0
0 8 0 7 0 0 0 2 0
0 0 0 6 5 8 0 0 0
0 9 0 0 0 4 0 8 0
0 0 2 1 0 0 0 0 0
3 0 1 5 0 9 0 7 0
4 0 0 0 0 8 0 0 0
The first row in the matrix 9 9 R 1 3 2 4 Þ 3 3 3 3 Rm contains submatrix no. 1 from m, the second row contains submatrix no. 2, etc.
Let's show this in colors:
m:
| 0 | 0 | 0 | 0 | 6 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 8 | 0 | 7 | 0 | 0 | 5 |
| 0 | 0 | 9 | 1 | 0 | 3 | 8 | 0 | 0 |
| 0 | 8 | 0 | 0 | 0 | 0 | 0 | 9 | 0 |
| 7 | 0 | 0 | 6 | 5 | 8 | 0 | 0 | 4 |
| 0 | 2 | 0 | 0 | 0 | 0 | 0 | 8 | 0 |
| 0 | 0 | 2 | 3 | 0 | 1 | 4 | 0 | 0 |
| 1 | 0 | 0 | 5 | 0 | 9 | 0 | 0 | 8 |
| 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 |
9 9 R 1 3 2 4 Þ 3 3 3 3 Rm:
| 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 9 |
| 0 | 6 | 0 | 8 | 0 | 7 | 1 | 0 | 3 |
| 0 | 0 | 0 | 0 | 0 | 5 | 8 | 0 | 0 |
| 0 | 8 | 0 | 7 | 0 | 0 | 0 | 2 | 0 |
| 0 | 0 | 0 | 6 | 5 | 8 | 0 | 0 | 0 |
| 0 | 9 | 0 | 0 | 0 | 4 | 0 | 8 | 0 |
| 0 | 0 | 2 | 1 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 1 | 5 | 0 | 9 | 0 | 7 | 0 |
| 4 | 0 | 0 | 0 | 0 | 8 | 0 | 0 | 0 |
The matrix t1 contains 81 rows and 27 columns.
We must now see which numbers that occur in each row.
We can't use the membership operator this time, as it operates on all rows of t1:
Rt1
81 27
:I9"Et1
1 1 1 1 1 1 1 1 1
Instead we create an outer product using the % operator: :I9"J.%t1:
R:I9"J.%t1
9 81 27
This is a big table, but APL stores a table of logical values using one bit per element.
We reduce it along the rows and negates:
T(/:I9"J.%t1
0 1 1 0 0 0 1 1 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 1 1 1 0 1 1 0 1 0 1 1 1 0 1 1 0 1 0 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1
1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1
1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 0 1 0 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 0 1 0 1 1 1 0 0 0 0 0 0
0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1
0 0 0 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 1 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0
1 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 0 1 1 1 0 0 0
1 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 0
0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 1 1 1 1 1 0 0 1
1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 0 1 1 1 1
0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 1 1 1 0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1 0 1 1 0 0 0
1 1 1 0 1 1 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0
1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0 0
0 0 0 1 1 0 1 0 1 0 0 0 1 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1 0 0 0 0 1 1 0 1 1 0 0 0 0 1 1 0 0 0 0
1 0 1 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 0 1
This is a matrix with dimensions 9 81. If element ;i<j' is true it means that the number i is a possible candidate for cell no. j. You can see from the first number in each row that the candidates for the first cell is: 2, 3, 5, and 8.
We call this matrix t2:
t2[T(/:I9"J.%t1
If we sum the rows and reshape to 9x9, and add 10 if the correponding cell in the original matrix is non-zero, we get this:
:9 9 R-/;1' t2"-10=m*0
4 4 5 3 13 3 5 5 5
13 3 3 12 2 11 5 4 15
3 3 13 12 2 13 13 4 3
3 15 5 3 4 2 6 16 5
12 3 2 12 14 11 3 3 13
4 16 5 3 4 1 5 15 4
4 4 14 10 1 11 14 3 3
12 4 4 12 2 13 4 4 14
5 5 5 2 13 3 6 5 5
You can see that this table contains two elements that are 1: Row 6, column 6, and row 7 column 5. It means that these two cells contain only a single candidate.
We can do other operations on the t2 matrix, but first we get rid of the cells that are already occupied:
t2[ 9 9 9 RÞt2) 9 81 Rm%0
Now t2;r<c<i' is true if the number i is a candidate in row r, column c.
If we reduce along dimension 2 we get:
-/;2' t2
5 6 6 3 4 0 5 2 3
4 3 4 0 0 4 0 0 2
0 4 0 2 2 4 3 0 0
4 5 5 4 3 4 3 0 0
4 2 4 0 0 0 0 0 1
4 0 5 4 3 4 3 0 3
0 0 0 0 3 4 3 2 3
0 3 4 3 0 4 4 0 0
3 5 6 4 5 7 0 2 4
This table contains a number 1 in row 5, column 9. It means that the number 9 is a single candidate in row 5.
We add along dimension 1:
-/;1' t2
0 2 4 0 6 5 0 3 3
3 0 5 2 4 5 4 0 3
5 0 7 4 4 5 2 2 0
0 3 0 4 0 0 2 0 2
2 4 2 4 0 0 0 1 2
0 3 0 4 1 1 0 0 0
6 6 7 0 3 5 4 0 3
4 6 5 2 2 5 4 0 0
4 4 4 0 0 5 5 0 3
This table contains a number 1 in row 5, column 8. It means that the number 8 is a single candidate in column 5. And we have two 1's in row 6: The numbers 5 and 6 occur only once in column 6.
In order to find the single occurances in the submatrices, we rearrange the matrix before adding:
-/;2' 9 9 9 R 1 3 2 4 5 Þ 3 3 3 3 9 Rt2
4 2 5 0 5 4 3 2 0
0 4 0 3 1 0 0 0 2
5 7 5 2 0 4 5 0 3
4 0 6 2 4 4 0 0 2
2 3 2 6 0 0 2 0 2
6 4 6 0 2 4 4 0 0
0 0 5 4 5 7 3 3 4
0 3 0 3 0 1 0 1 0
3 5 5 0 3 7 4 0 3
Now we have a number 1 in row 2, column 5. It means that the number 5 occurs once in submatrix 2, and we have two 1's in row 8, the numbers 6 and 8 occur once in submatrix 8.
We now have all the tools ready to assemble the program that uses the new algorithms. We still keep the brute force algorithm as a fallback, but with one improvement: Instead of just take the first zero in the matrix and try all possible candidates, we select the unoccupied cell that has fewest possible candidates.
Let's take a look at the final program:
G sudoku m<r<c<m1<t1<t2<t3<i
;1' t1[m;,Þ 9 9 RI9<'
;2' t1[t1,Þm;<81RI9'
;3' t1[t1,:9 9 R 1 3 2 4 Þ 3 3 3 3 Rm";, 2 4 1 3 Þ 3 3 3 3 RI9<'
;4' t2[T(/:I9"J.%t1
;5' t1[,:9 9 R-/;1' t2"-10=m*0
;6' t2[ 9 9 9 RÞt2) 9 81 Rm%0
;7' {l1=sudoku1
;8' {l2=sudoku2
;9' {l2=sudoku3
;10' {l2=sudoku4
;11' {l2=sudoku5
;12' {l2=sudoku6
;13' l1>m
;14' I0
;15' {0
;16' l2>i[Rt1
;17' l3>{:i%0"/0
;18' m1[m
;19' m1;r<c'[t1;i'
;20' sudoku m1
;21' i[i_1
;22' {l3
G
It has been split up in several programs to make it easier to read. The programs sudoku1 to sudoku6 each test for a specific condition and returns either I0 or 1. So if sudoku1 returns 1, we jump to the label l1.
The program sudoku1 looks like this:
G z[sudoku1
;1' r[:ßt1";1'
;2' z[I0
;3' {:t1;r'$9"/0
;4' z[1
G
We sort the number of candidates and assign the number of the first to r. If this number is larger than 9 it means that there are no zeros left in the puzzle. In the main program we jump to label l1 and print the solution.
In sudoku2 we look for cells with a single candidate:
G z[sudoku2
;1' z[I0
;2' {:t1;r'&1"/0
;3' z[1
;4' c[t1;r'
;5' t1[I0
;6' {:c%0"/0
;7' c[1-9M:r_1"
;8' r[1-D:r_1"+9
;9' t1[,-/t2;r<c<'=I9
G
In line two we check that t1;r' is one, else we quit and go on to the next algorithm.
In line six we check if cell with fewest candidates has zero candidates. If this is the case we return an empty vector in t1 and the main program exits: We have reached a dead end.
Else we calculate the row and column number and assign the candidate number to t1. The comma in front makes sure that t1 is a vector of lenght one, and not a scalar.
sudoku3 looks for candidates that occur once in a row. It looks like this:
G z[sudoku3
;1' z[I0
;2' t3[-/;2' t2
;3' i[:,t3"I1
;4' {:i%82"/0
;5' z[1
;6' t1[,1-9M:i_1"
;7' r[1-D:i_1"+9
;8' c[-/:,t2;r<<t1'"=I9
G
In line 3 we look for the first occurrence of the number 1. If none exist, we exit in line 4. Else we assign the candidate number to t1 and calculates the row and column numbers.
sudoku4
G z[sudoku4
;1' z[I0
;2' t3[-/;1' t2
;3' i[:,t3"I1
;4' {:i%82"/0
;5' z[1
;6' t1[,1-9M:i_1"
;7' c[1-D:i_1"+9
;8' r[-/:,t2;<c<t1'"=I9
G
And sudoku5 checks the submatrices:
G z[sudoku5<r1<c1
;1' z[I0
;2' t3[-/;2' 9 9 9 R 1 3 2 4 5 Þ 3 3 3 3 9 Rt2
;3' i[:,t3"I1
;4' {:i%82"/0
;5' z[1
;6' t1[,1-9M:i_1"
;7' r1[ 3 3 ND:i_1"+9
;8' c1[ 3 3 N@1--/:,:9 9 9 R 1 3 2 4 5 Þ 3 3 3 3 9 Rt2";1- 3 3 Br1<<t1'"=I9
;9' r[1-c1;1'-3=r1;1'
;10' c[1-c1;2'-3=r1;2'
G
We use the N operator to convert the index into base 3 numbers, and the B operator to convert back again:
3 3 N0
0 0
3 3 N1
0 1
3 3 N2
0 2
3 3 N3
1 0
3 3 N4
1 1
3 3 N5
1 2
3 3B1 2
5
The last program sudoku6 contains the brute force algorithm:
G z[sudoku6
;1' z[1
;2' c[1-9M:r_1"
;3' r[1-D:r_1"+9
;4' t1[:T:I9"E:m;r<',m;<c',,m;:3=D::@1-r"+3""-I3<:3=D::@1-c"+3""-I3'""/I9
G
When sudoku6 is called, r points to the cell with the fewest number of candidates. We return the list in the vector t1.
Now the program is finished - is it faster?
time
0 0 1
sudoku o1
8 1 7 2 6 5 9 4 3
4 6 3 8 9 7 2 1 5
2 5 9 1 4 3 8 7 6
6 8 4 7 3 2 5 9 1
7 9 1 6 5 8 3 2 4
3 2 5 9 1 4 6 8 7
5 7 2 3 8 1 4 6 9
1 4 6 5 2 9 7 3 8
9 3 8 4 7 6 1 5 2
time
0 3 54
Yes, ten times faster than before.
We can try a more difficult problem:
o2[a2n K800000000003600000070090200050007000000045700000100030001000068008500010090000400K
time
0 0 0
sudoku o2
8 1 2 7 5 3 6 4 9
9 4 3 6 8 2 1 7 5
6 7 5 4 9 1 2 8 3
1 5 4 2 3 7 8 9 6
3 6 9 8 4 5 7 2 1
2 8 7 1 6 9 5 3 4
5 2 1 9 7 4 3 6 8
4 3 8 5 2 6 9 1 7
7 9 6 3 1 8 4 5 2
time
1 49 4
It took 109 seconds. It would take hours using only the brute force algorithm.
I'll close my little APL corner here. You can continue and try to implement the other sudoku algorithms in APL yourself!
"off
010 14.12.07 03/10/14 mk
connected 6.25.35 to date 52.03.29
cpu time 0.01.57 to date 1.16.35